This fall I am teaching Mathematical Methods for Scientist. This week we started to talk about differential equations and for the lecture I was looking for an example of a broadely used first order ODE: my final choice has been the logistic equation.

It is a fairly simple differential equation that is used to describe the growth (and saturation) of populations in environments with competition for limited resources. Before entering into more details I think it’s time to digress slightly and talk about something simpler.

###How can one describe the growth of a population of bacteria (assuming that they do not die)?

We could start by thinking that the rate of growth of the population of bacteria is proportional to the existing number of cells. In this case we would consider the equation

$$ \frac{dP}{dt} = r P(t) $$

where where $r > 0$ describes the growth rate and $P(t)$ is the quantity describing the number of cells at time $t$ (the population size).

The solution of such equation is a simple exponential (if you don’t trust me, trust at least wolfram alpha):

$$ P(t) = c e^{rt}. $$

Now, if we know that the population of bacteria at time $t=0$ consists of $P_0>0$ cells (e.g. $10$), we can take it as initial condition and get

$$ c = P_0, $$

as one would expect. And therefore we could predict how many bacteria we can count at a certain time $t$ using

$$ P(t) = P_0 e^{rt}. $$

While bacteria are very small and it would take a long time for them to consume all the food and all the available space, it seems clear that this model is extremely unralistic when we consider the growth of a population of bigger entities (e.g. humans, rabbits, mices, economy, users of facebook, …). Clearly for such systems the finiteness of the resourcces (e.g. space or nutrition) would become soon apparent.

Doesn’t it!?! Think about it, our whole economic system is blindly based on the fact that economy/production/population/consumes can keep growing forever… Something sounds wrong: at a certain point it will be clear that our resources are finite. What will happen then (assuming that it’s not too late to do something)?

Anyway… Let’s forget about catastrophes and let’s go back to our model

# A slightly improved model for population growth

To describe the growth of a population in an environment with competition for limited resources we need to modify the equation above and include a term that slows down the growth when the population becomes too big with respect to the resources.

This equation is called logistic equation (sometimes you find it as Verhulst equation):

$$ \frac{d P}{dt} = r P(t) \left(1 - \frac{P(t)}{K}\right) $$

where $r>0$ is the rate of growth (as before) and $K > P_0$ is a parameter that measures what is the maximal amount of resources (or, from a different point of view, how big our population can become).

Separating variables we can easily solve the equation and, with some algebra we get

$$ \frac{K P}{K-P} = \frac{P}{1-P/K} = C e^{rt}. $$

As for the bacteria, let’s say that at time $t=0$ our population consists of $0 < P_0 < K$ individuals. Then we easily get

$$ C = \frac{K P_0}{K - P_0} $$

and therefore (with few other algebraic steps) we get as solution the logistic function:

$$ P(t) = \frac{ K P_0 e^{rt} }{ K + P_0 ( e^{rt} -1 )}. $$

If you compare this solution with the exponential growth of the bacteria you can notice that there is a huge difference. The logistic growth presents an horizontal asymptote for $t\to \infty$, i.e. the population grows slower and slower until it saturates the environment and is not able to grow anymore.

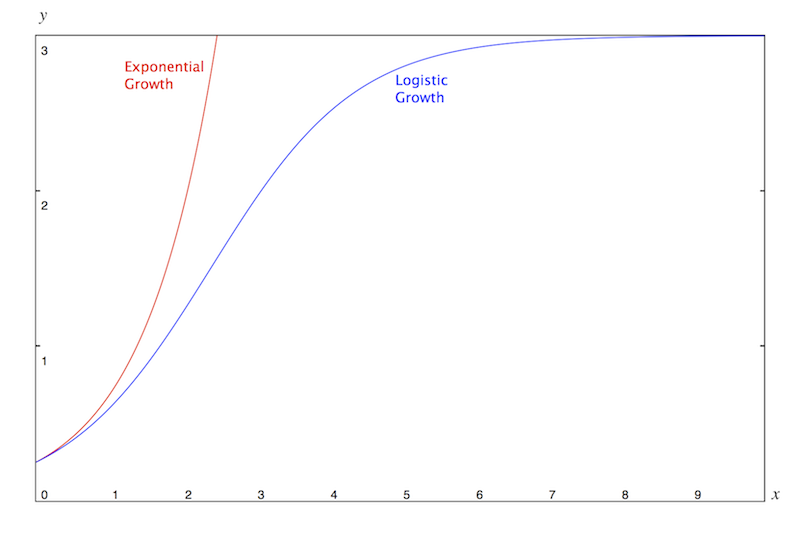
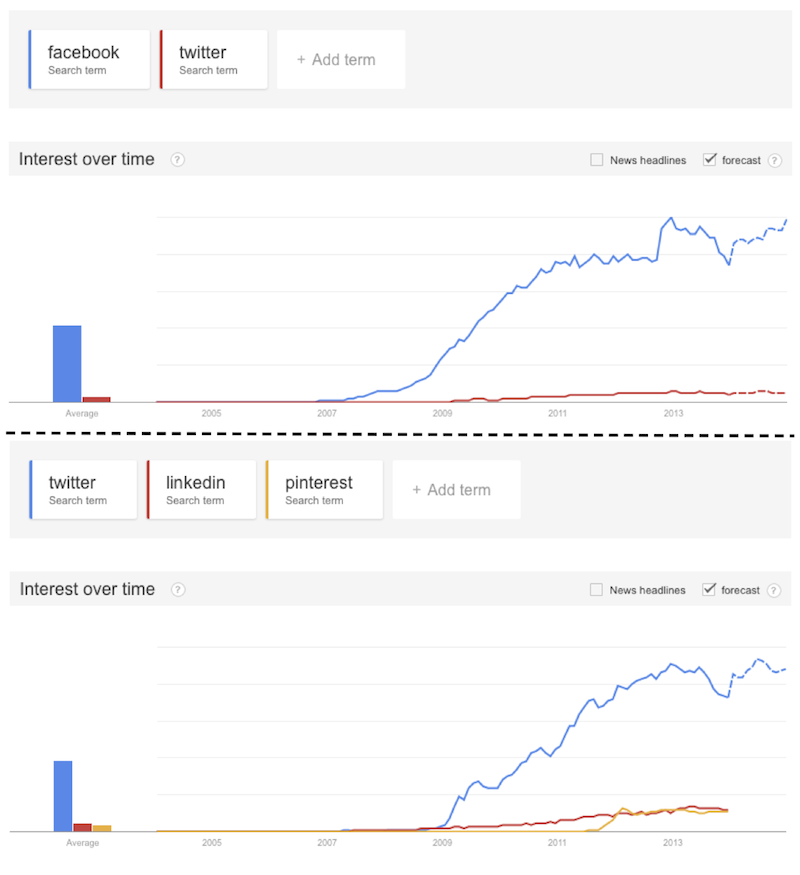
Remember this graph when you look to graphs describing the incredible growth of something. You should not be surprised if you recognise it.

Make an experiment, look to a graph of the diffusion of internet on your country (or in the world), or to one about the production of crops or oil, or to the Google Trends graph of searches for different social networks.

Note that if you set $K=2A/B$, $r=B$ and $P_0 = K/(1+e^{BC})$, for some numbers $A,B,C$ whose meaning I don’t really know, you obtain the equation of the Hubbert Model of Oil Production that is used to predict when the maximum of oil production will be reached and how the production will behave afterward.

Note, moreover, that in the limit $K\to+\infty$ we go back to the exponential growth model.

Finally, do not confuse this logistic equation with the logistic map. They are strictly related but the study of the logistic map is a completely different story.